Stopping Agents

Language agents for optimal stopping

Theory

We summarize the theory underlying stopping agents below, and delegate to our paper for a more detailed discussion.

1. The Optimal Stopping Objective

The classical discrete-time finite-horizon optimal stopping objective with decision opportunities at $t=1,\dots,T$ is given by,

$J(\theta) = \mathbb{E}[\sum_{t=1}^{\tau-1} w_t + q_\tau], \qquad (1)$

where $\theta$ are the parameters of the stopping policy $\pi_\theta$ and $\tau$ is the stopping time induced by this policy. $w_t$ and $q_\tau$ are the waiting and stopping rewards, and Equation 1 is the expected cumulative reward.

2. Language Agents for Optimal Stopping

Stopping agents are language models that solve discrete-time finite-horizon optimal stopping problems with textual state spaces. Stopping agents are trained via imitation learning, and not reinforcement learning.

Why not dynamic programming?

In principle, the optimal stopping problem in Equation 1 can be solved exactly using dynamic programming¹. But when the state-space is high-dimensional, like text, dynamic programming suffers from the curse of dimensionality, and we need to parameterize the stopping policy.

Why language models?

For textual state spaces, pretrained large language models are a compelling parameterization, given their demonstrated performance on various natural language understanding tasks. Specifically, we would like to train a large language model $\pi_\theta(a_t|s_t)$ that observes the conversation transcript $s_t$ and generates an action $a_t \in$ {wait, quit} at each $t=1,\dots,T$ to maximize the expected cumulative reward.

Why not reinforcement learning?

While a natural training approach is via reinforcement learning, reinforcement learning with language model policies is notoriously unstable, sensitive to implementation details², and challenging to scale. Moreover, our setting requires multi-turn reinforcement learning, which suffers from issues such as entropy collapse and gradient norm explosions, and remains an open research problem³.

3. Imitation Learning to Quit

Imitation learning (behavioral cloning in particular) trains a policy to mimic the actions of an expert policy by learning from a dataset of optimal state-action trajectories. Imitation learning is an effective alternative to reinforcement learning, but requires a large dataset of optimal state-action pairs, which is usually difficult to acquire.

Inferring optimal state-action trajectories

Our key insight is that, for optimal stopping problems, we can infer optimal state-action trajectories from historical suboptimal data.

Consider a sales call stopping agent with 2 decision opportunities, at t=30 and at t=60 seconds, which incurs a waiting cost of C per second and obtains a reward of B if it allows a successful call to proceed to the end without stopping, and a reward of 0 otherwise.

Now consider a historical conversation in the training data L seconds long that ended in a sale. The stopping agent has 3 candidate stopping decisions, and the reward for each of these can be calculated exactly:

Candidate Stopping Decision	Reward
Stop at t=30	-30C
Stop at t=60	-60C
Never stop	B - LC

The optimal state-action trajectory can directly be derived from the candidate stopping decision that maximizes the reward. Let’s say B - LC > -30C > -60C, so it is optimal to never stop. The optimal state-action trajectory is given by the following state-action pairs:

State $s_t \equiv$ transcript until t	Optimal Action $a^*_t$
$s_{30}$	wait
$s_{60}$	wait

We do the above for all training conversations to construct a dataset of pairs of states (partial conversation transcripts) and optimal actions (wait or quit).

Imitation learning via fine-tuning

Given the aforementioned dataset, we train the large language model $\pi_\theta$ to generate the optimal action $a_t$ given the state $s_t$ by fine-tuning to minimize the cross-entropy loss $\mathbb{E}[-\textrm{log}~\pi_\theta(a^*_t|s_t)]$.

In practice, we wrap the state in a prompt to better leverage instruction-tuned language models. Below is an example of the prompt we use for optimal stopping of sales conversations in our paper.

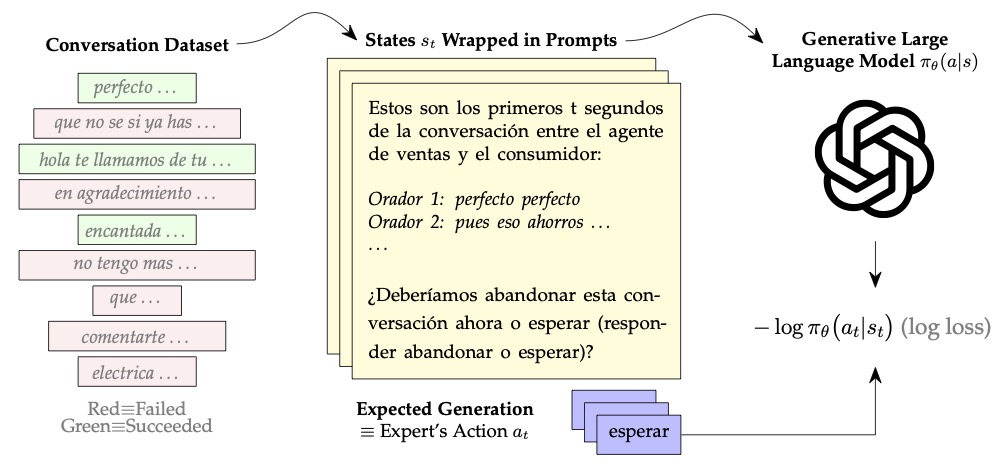
This prompt translates to:

Below are the first t seconds of the conversation between the sales agent Speaker 0 and the customer Speaker 1. [… conversation transcript follows …] Should we quit this conversation now or wait (respond with quit or wait):

Backward-induction threshold tuning

Fine-tuning gives us a stochastic policy that outputs probabilities $\pi_\theta(\cdot|s_t)$. To use this policy, we need to threshold the probabilities as: quit if $\pi_\theta($quit$|s_t) \geq \lambda_t$, wait otherwise, for some thresholds $\lambda_t$.

One approach to find the optimal thresholds is via grid-search on a validation set. However, this takes forever in practice. So we came up with a scalable solution called backward-induction threshold tuning.

The idea behind this approach is to first find the optimal threshold $\lambda_T$ for the final decision opportunity at $t=T$, and then find the optimal threshold for each $t=T-1, T-2, \dots, 1$ in reverse order, because a conversation that is not quit at t proceeds according to the already-set thresholds at $t+1, t+2, \dots, T$. Algorithm 1 in our paper describes this in more detail.

---